| ||||||||||||||||||||||||
Hambatan
atau resistansi berguna untuk mengatur besarnya kuat arus listrik yang
mengalir melalui suatu rangkaian listrik. Dalam radio dan televisi,
resistansi berguna untuk menjaga kuat arus dan tegangan pada nilai
tertentu dengan tujuan agar komponen-komponen listrik lainnya dapat
berfungsi dengan baik.
Untuk berbagai jenis kawat, panjang kawat dan penampang berbeda terdapat hubungan sebagai berikut:
Untuk mempermudah Anda mengenal berbagai macam jenis logam dan hambatan jenisnya, Anda perhatikan tabel di bawah ini!
Tabel –1. Hambatan jenis beberapa zat.  |
Hubungan antara hambatan kawat dengan jenis kawat dan ukuran kawat
Diposting oleh
Unknown
on Minggu, 21 April 2013
/
Comments: (0)
JEMBATAN WHEATSTONE
Diposting oleh
Unknown
/
Comments: (0)
Apa itu jembatan wheatstone?
Meskipun namanya jembatan tapi jembatan
yang satu ini bukan berbentuk konstruksi jembatan yang sering kita
lihat. yang menghubungkan dua tempat terpisah karena sesuatu (misal
jembatan di sungai). Istilah jembatan wheatstone dipakai dalam rangkaian elektronika untuk menyebut suatu rangkaian komponen elektronika.

Jembatan Wheatstone
Wheatstone Bridge
Wheatstone Bridge
Rangkaian elektrik ini dibuat oleh Samuel Hunter Christie pada tahun 1833 dan dikembangkan lebih lanjut dan dipopulerkan oleh Sir Charles Wheatstone pada tahun 1843 sehingga terkenal dengan jembatan wheatstone. Gunanya adalah untuk mengukur hambatan dengan cara menyeimbangkan kedua sisi rangkaian jembatan (bridge circuit).
Satu sisi jembatan terdapat komponen yang tak diketahui nilai
resistansinya sedangkan sisi lain diketahui nilai resistansinya. Operasi
ini juga mirip dengan potensiometer. Jembatan ini dibuat dengan merangkai empat buah hambatan dalam susunan seperti gambar di atas ini.
Operasi
Pada gambar di atas, Rx adalah komponen
yang ingin diketahui hambatannya. R1, R2, dan R3 adalah resistor yang
diketahui hambatannya dan hambatan pada R2 dapat diubah dan disesuaikan.
Jika perbandingan antara kedua hambatan di sisi yang diketahui (R2/R1)
sama dengan perbandingan sisi yang dicari, tegangan antara kedua titik potong (B dan D) akan menjadi nol dan tak ada arus listrik yang mengalir melalui galvanometer
Vg. Jika jembatan tak seimbang (atau nilai salah satu sisi hambatan
lebih besar dari hambatan lainnya), arah arus yang mengalir akan
mengindikasikan apakah R2 terlalu tinggi atau terlalu rendah. R2 akan bervariasi atau diubah-ubah nilainya sampai tidak ada arus mengalir melalui galvanometer, yang berarti terbaca nol.
Pada posisi seimbang, perbandingan antara R2 / R1 = Rx / R3
Atau dapat ditulis Rx = (R2 / R1) x R3
Selain itu, jika R1, R2 dan R3 diketahui
namun R2 tidak dapat diubah-ubah nilai hambatannya, perbedaan tegangan
yang ada atau arus yang mengalir melalui galvanometer dapat digunakan
untuk mengukur nilai Rx. Hmmm… gimana caranya? Kita dapat menggunakan hukum Kirchoff (disebut juga dengan aturan Kirchoff) untuk melakukannya.
MOMENTUM DAN IMPLUS
Diposting oleh
Unknown
on Rabu, 17 April 2013
/
Comments: (0)
1. Peluncuran Roket
Sebuah roket diluncurkan vertikal ke atas menuju atmosfer Bumi. Hal ini dapat dilakukan karena adanya gaya dorong dari mesin roket yang bekerja berdasarkan impuls yang diberikan oleh roket. Pada saat roket sedang bergerak, akan berlaku hukum kekekalan momentum. Pada saat roket belum dinyalakan, momentum roket adalah nol. Apabila bahan bakar di dalamnya telah dinyalakan, pancaran gas mendapatkan momentum yang arahnya ke bawah. Oleh karena momentum bersifat kekal, roket pun akan mendapatkan momentum yang arahnya berlawanan dengan arah buang bersifat gas roket tersebut dan besarnya sama. Secara matematis gaya dorong pada roket dinyatakan dalam hubungan berikut.
Impuls = perubahan momentum
FΔt = Δ(mv)
F = v(Δm/ Δt)
dengan: F = gaya dorong roket (N),
(Δm/ Δt)= perubahan massa roket terhadap waktu (kg/s), dan
v = kecepatan roket (m/s).
2. Air Safety Bag (kantong udara)
Air Safety Bag (kantong udara) digunakan untuk memperkecil gaya akibat tumbukan yang terjadi pada saat tabrakan. Kantong udara tersebut dipasangkan pada mobil serta dirancang untuk keluar dan mengembang secara otomatis saat tabrakan terjadi. Kantong udara ini mampu meminimalkan efek gaya terhadap benda yang bertumbukan. Prinsip kerjanya adalah memperpanjang waktu yang dibutuhkan untuk menghentikan momentum pengemudi. Saat tabrakan terjadi, pengemudi cenderung untuk tetap bergerak sesuai dengan kecepatan gerak mobil (Hukum Pertama Newton). Gerakan ini akan membuatnya menabrak kaca depan mobil yang mengeluarkan gaya sangat besar untuk menghentikan momentum pengemudi dalam waktu sangat singkat. Apabila pengemudi menumbuk kantong udara, waktu yang digunakan untuk menghentikan momentum pengemudi akan lebih lama sehingga gaya yang ditimbulkan pada pengemudi akan mengecil. Dengan demikian, keselamatan si pengemudi akan lebih terjamin.
3. Desain Mobil
Desain mobil dirancang untuk mengurangi besarnya gaya yang timbul akibat tabrakan. Caranya dengan membuat bagian-bagian pada badan mobil agar dapat menggumpal sehingga mobil yang bertabrakan tidak saling terpental satu dengan lainnya. Mengapa demikian? Apabila mobil yang bertabrakan saling terpental, pada mobil tersebut terjadi perubahan momentum dan impuls yang sangat besar sehingga membahayakan keselamatan jiwa penumpangnya.
Daerah penggumpalan pada badan mobil atau bagian badan mobil yang dapat penyok akan memperkecil pengaruh gaya akibat tumbukan yang dapat dilakukan melalui dua cara, yaitu memperpanjang waktu yang dibutuhkan untuk menghentikan momentum mobil dan menjaga agar mobil tidak saling terpental. Rancangan badan mobil yang memiliki daerah penggumpalan atau penyok tersebut akan mengurangi bahaya akibat tabrakan pada penumpang mobil.
Beberapa aplikasi Hukum Kekekalan Momentum lainnya adalah bola baja yang diayunkan dengan rantai untuk menghancurkan dinding tembok. Benturan meteor terhadap Bumi dapat dilihat di kawah Barringer, Winlow, Arizona, Amerika Serikat. Bola golf yang dipukul dengan stik golf juga menggunakan Hukum Kekekalan Momentum.
THERMODINAMIKA
Diposting oleh
Unknown
/
Comments: (0)
Hukum Pertama Termodinamika
Perubahan energi dalam: 
Keterangan:
 :Perubahan energi dalam (Joule)
:Perubahan energi dalam (Joule)- U2:Energi dalam pada keadaan akhir (Joule)
- U1:Energi dalam pada keadaan awal (Joule)
- p: Besarnya tekanan (atm)
 : Perubahan volume (liter)
: Perubahan volume (liter)

Penghitungan energi dalam:
- Gas monoatomik:

- Gas diatomik:

Proses-proses termodinamika gas
Proses isobarik
Proses isobarik adalah perubahan keadaan gas pada tekanan tetap.Persamaan keadaan isobarik:
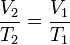
Usaha yang dilakukan pada keadaan isobarik:

Proses isokhorik
Persamaan keadaan isokhorik:

Proses isotermis/isotermik
Proses isotermik adalah perubahan keadaan gas pada suhu tetap.Persamaan keadaan isotermik:
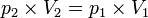
Usaha yang dilakukan pada keadaan isotermik:
- Dari persamaan gas ideal

- Rumus umum usaha yang dilakukan gas:

maka:

karena
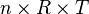 bernilai tetap, maka:
bernilai tetap, maka:
Ingat integral ini!

maka persamaan di atas menjadi
Proses adiabatik
Proses adiabatik adalah perubahan keadaan gas dimana tidak ada kalor yang masuk maupun keluar dari sistem.Persamaan keadaan adiabatik:

Tetapan Laplace:
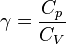
karena
 , maka persamaan diatas dapat juga ditulis:
, maka persamaan diatas dapat juga ditulis:
MEKANIKA FLUIDA
Diposting oleh
Unknown
/
Comments: (0)
Mekanika fluida mengasumsikan bahwa semua fluida mengikuti:
- Hukum kekekalan massa
- Hukum kekekalan momentum
- Hipotesis kontinum, yang dijelaskan di bagian selanjutnya.
Selain itu, kadang-kadang viskositas dari suatu fluida dapat diasumsikan bernilai nol (fluida tidak viskos). Terkadang gas juga dapat diasumsikan bersifat tidak viskos. Jika suatu fluida bersifat viskos dan alirannya ditampung dalam suatu cara (seperti dalam pipa), maka aliran pada batas sistemnya mempunyai kecepatan nol. Untuk fluida yang viskos, jika batas sistemnya tidak berpori, maka gaya geser antara fluida dengan batas sistem akan memberikan resultan kecepatan nol pada batas fluida.
Hipotesis kontinum
Fluida disusun oleh molekul-molekul yang bertabrakan satu sama lain. Namun demikian, asumsi kontinum menganggap fluida bersifat kontinu. Dengan kata lain, properti seperti densitas, tekanan, temperatur, dan kecepatan dianggap terdefinisi pada titik-titik yang sangat kecil yang mendefinisikan REV (‘’Reference Element of Volume’’) pada orde geometris jarak antara molekul-molekul yang berlawanan di fluida. Properti tiap titik diasumsikan berbeda dan dirata-ratakan dalam REV. Dengan cara ini, kenyataan bahwa fluida terdiri dari molekul diskrit diabaikan.Hipotesis kontinum pada dasarnya hanyalah pendekatan. Sebagai akibatnya, asumsi hipotesis kontinum dapat memberikan hasil dengan tingkat akurasi yang tidak diinginkan. Namun demikian, bila kondisi benar, hipotesis kontinum menghasilkan hasil yang sangat akurat.
Masalah akurasi ini biasa dipecahkan menggunakan mekanika statistik. Untuk menentukan perlu menggunakan dinamika fluida konvensial atau mekanika statistik, angka Knudsen permasalahan harus dievaluasi. Angka Knudsen didefinisikan sebagai rasio dari rata-rata panjang jalur bebas molekular terhadap suatu skala panjang fisik representatif tertentu. Skala panjang ini dapat berupa radius suatu benda dalam suatu fluida. Secara sederhana, angka Knudsen adalah berapa kali panjang diameter suatu partikel akan bergerak sebelum menabrak partikel lain.
Persamaan Navier-Stokes
Persamaan Navier-Stokes (dinamakan dari Claude-Louis Navier dan George Gabriel Stokes) adalah serangkaian persamaan yang menjelaskan pergerakan dari suatu fluida seperti cairan dan gas. Persamaan-persamaan ini menyatakan bahwa perubahan dalam momentum (percepatan) partikel-partikel fluida bergantung hanya kepada gaya viskos internal (mirip dengan gaya friksi) dan gaya viskos tekanan eksternal yang bekerja pada fluida. Oleh karena itu, persamaan Navier-Stokes menjelaskan kesetimbangan gaya-gaya yang bekerja pada fluida.Persamaan Navier-Stokes memiliki bentuk persamaan diferensial yang menerangkan pergerakan dari suatu fluida. Persaman seperti ini menggambarkan hubungan laju perubahan suatu variabel terhadap variabel lain. Sebagai contoh, persamaan Navier-Stokes untuk suatu fluida ideal dengan viskositas bernilai nol akan menghasilkan hubungan yang proposional antara percepatan (laju perubahan kecepatan) dan derivatif tekanan internal.
Untuk mendapatkan hasil dari suatu permasalahan fisika menggunakan persamaan Navier-Stokes, perlu digunakan ilmu kalkulus. Secara praktis, hanya kasus-kasus aliran sederhana yang dapat dipecahkan dengan cara ini. Kasus-kasus ini biasanya melibatkan aliran non-turbulen dan tunak (aliran yang tidak berubah terhadap waktu) yang memiliki nilai bilangan Reynold kecil.
Untuk kasus-kasus yang kompleks, seperti sistem udara global seperti El Niño atau daya angkat udara pada sayap, penyelesaian persamaan Navier-Stokes hingga saat ini hanya mampu diperoleh dengan bantuan komputer. Kasus-kasus mekanika fluida yang membutuhkan penyelesaian berbantuan komputer dipelajari dalam bidang ilmu tersendiri yaitu mekanika fluida komputasional
Bentuk umum persamaan
Bentuk umum persamaan Navier-Stokes untuk kekekalan momentum adalah : adalah densitas fluida,
adalah densitas fluida,
 adalah derivatif substantif (dikenal juga dengan istilah derivatif dari material)
adalah derivatif substantif (dikenal juga dengan istilah derivatif dari material)
 adalah vektor kecepatan,
adalah vektor kecepatan, adalah vektor gaya benda, dan
adalah vektor gaya benda, dan adalah tensor yang menyatakan gaya-gaya permukaan yang bekerja pada partikel fluida.
adalah tensor yang menyatakan gaya-gaya permukaan yang bekerja pada partikel fluida.
 adalah tensor yang simetris kecuali bila fluida tersusun dari derajat
kebebasan yang berputar seperti vorteks. Secara umum, (dalam tiga
dimensi)
adalah tensor yang simetris kecuali bila fluida tersusun dari derajat
kebebasan yang berputar seperti vorteks. Secara umum, (dalam tiga
dimensi)  memiliki bentuk persamaan:
memiliki bentuk persamaan: adalah tegangan normal, dan
adalah tegangan normal, dan adalah tegangan tangensial (tegangan geser).
adalah tegangan tangensial (tegangan geser).
Fluida Newtonian vs. non-Newtonian
Sebuah Fluida Newtonian (dinamakan dari Isaac Newton) didefinisikan sebagai fluida yang tegangan gesernya berbanding lurus secara linier dengan gradien kecepatan pada arah tegak lurus dengan bidang geser. Definisi ini memiliki arti bahwa fluida newtonian akan mengalir terus tanpa dipengaruhi gaya-gaya yang bekerja pada fluida. Sebagai contoh, air adalah fluida Newtonian karena air memiliki properti fluida sekalipun pada keadaan diaduk.Sebaliknya, bila fluida non-Newtonian diaduk, akan tersisa suatu "lubang". Lubang ini akan terisi seiring dengan berjalannya waktu. Sifat seperti ini dapat teramati pada material-material seperti puding. Peristiwa lain yang terjadi saat fluida non-Newtonian diaduk adalah penurunan viskositas yang menyebabkan fluida tampak "lebih tipis" (dapat dilihat pada cat). Ada banyak tipe fluida non-Newtonian yang kesemuanya memiliki properti tertentu yang berubah pada keadaan tertentu.
Persamaan pada fluida Newtonian
Konstanta yang menghubungkan tegangan geser dan gradien kecepatan secara linier dikenal dengan istilah viskositas. Persamaan yang menggambarkan perlakuan fluida Newtonian adalah: adalah tegangan geser yang dihasilkan oleh fluida
adalah tegangan geser yang dihasilkan oleh fluida adalah viskositas fluida-sebuah konstanta proporsionalitas
adalah viskositas fluida-sebuah konstanta proporsionalitas adalah gradien kecepatan yang tegak lurus dengan arah geseran
adalah gradien kecepatan yang tegak lurus dengan arah geseran
 adalah tegangan geser pada bidang
adalah tegangan geser pada bidang  dengan arah
dengan arah 
 adalah kecepatan pada arah
adalah kecepatan pada arah 
 adalah koordinat berarah
adalah koordinat berarah 


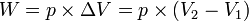



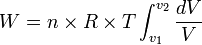
![W = n \times R \times T \times[\ln V_2 - \ln V_1]](http://upload.wikimedia.org/math/0/a/7/0a71834fa480baf975b62a9a64bb7b7d.png)